演奏性の向上を目指して-平均律とフレット長
ピタゴラス音律以来、1オクターブは12分割されることになりました。純正律も同様に12分割されていますが、ピタゴラス音律同様、音と音の振動比が一定でないために、移調ができないなどの演奏上の問題がありました。それぞれの音の周波数比を一定し、1オクターブを12分割するためには、以下の式を満たすXを求めれば良いことになります。
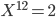
![X=\sqrt[12]{2}=1.059463...](https://smaeda.com/wp-content/plugins/latex/cache/tex_8e318469d050b7abaa8f8b7d9b5d5006.gif)
平均律の全ての音の並びは以下の表のようになります。
| 音名 | 弦長 | 振動数 |
| C | ![\frac{1}{\sqrt[12]{2}^{0}}](https://smaeda.com/wp-content/plugins/latex/cache/tex_3677790f818585e8b359b043de81180a.gif) = 1.0000 = 1.0000 |
![\sqrt[12]{2}^{0}](https://smaeda.com/wp-content/plugins/latex/cache/tex_5e07cec1a6e466ca06ddc280b444e5dc.gif) = 1.0000 = 1.0000 |
| C# | ![\frac{1}{\sqrt[12]{2}^{1}}](https://smaeda.com/wp-content/plugins/latex/cache/tex_37b7c9e5bb44c5cb3bfdc9f094107cea.gif) = 0.9439 = 0.9439 |
![\sqrt[12]{2}^{1}](https://smaeda.com/wp-content/plugins/latex/cache/tex_f10851103d3cb31c1385ef91a26c9360.gif) = 1.0595 = 1.0595 |
| D | ![\frac{1}{\sqrt[12]{2}^{2}}](https://smaeda.com/wp-content/plugins/latex/cache/tex_2d026556715415ab647f23bbf8f69c8d.gif) = 0.8909 = 0.8909 |
![\sqrt[12]{2}^{2}](https://smaeda.com/wp-content/plugins/latex/cache/tex_32df5f536808fb706241fa8553dedd25.gif) = 1.1225 = 1.1225 |
| D# | ![\frac{1}{\sqrt[12]{2}^{3}}](https://smaeda.com/wp-content/plugins/latex/cache/tex_a6ad433de3578a36afe5e71a31459b4b.gif) = 0.8409 = 0.8409 |
![\sqrt[12]{2}^{3}](https://smaeda.com/wp-content/plugins/latex/cache/tex_965d22b7880b0eae694def8391c41668.gif) = 1.1892 = 1.1892 |
| E | ![\frac{1}{\sqrt[12]{2}^{4}}](https://smaeda.com/wp-content/plugins/latex/cache/tex_c8176515ab474d9860b96c82596fe665.gif) = 0.7937 = 0.7937 |
![\sqrt[12]{2}^{4}](https://smaeda.com/wp-content/plugins/latex/cache/tex_aeb520bbfa8c5eea5f3e547f43fb1e52.gif) = 1.2599 = 1.2599 |
| F | ![\frac{1}{\sqrt[12]{2}^{5}}](https://smaeda.com/wp-content/plugins/latex/cache/tex_57e99384388599abe02882377443139c.gif) = 0.7492 = 0.7492 |
![\sqrt[12]{2}^{5}](https://smaeda.com/wp-content/plugins/latex/cache/tex_b9c7d1df537d7a8f2082b856cd64f58c.gif) = 1.3348 = 1.3348 |
| F# | ![\frac{1}{\sqrt[12]{2}^{6}}](https://smaeda.com/wp-content/plugins/latex/cache/tex_03cf015edb07d85f35a23ed6544ab1b6.gif) = 0.7071 = 0.7071 |
![\sqrt[12]{2}^{6}](https://smaeda.com/wp-content/plugins/latex/cache/tex_e1aab953250605d8abb4ad6650603f95.gif) = 1.4142 = 1.4142 |
| G | ![\frac{1}{\sqrt[12]{2}^{7}}](https://smaeda.com/wp-content/plugins/latex/cache/tex_53c7c8d5f5da92f43f34bce7d5f6d737.gif) = 0.6674 = 0.6674 |
![\sqrt[12]{2}^{7}](https://smaeda.com/wp-content/plugins/latex/cache/tex_64726bf764bab6d874593c0d6b8ca0f2.gif) = 1.4983 = 1.4983 |
| G# | ![\frac{1}{\sqrt[12]{2}^{8}}](https://smaeda.com/wp-content/plugins/latex/cache/tex_c84acbec18597c9c69696ca69ddd04e5.gif) = 0.6300 = 0.6300 |
![\sqrt[12]{2}^{8}](https://smaeda.com/wp-content/plugins/latex/cache/tex_ba621ed6545747bfc52eb841e6a63df3.gif) = 1.5874 = 1.5874 |
| A | ![\frac{1}{\sqrt[12]{2}^{9}}](https://smaeda.com/wp-content/plugins/latex/cache/tex_34d76ac991e81b205740e1be2fbd1ef3.gif) = 0.5946 = 0.5946 |
![\sqrt[12]{2}^{9}](https://smaeda.com/wp-content/plugins/latex/cache/tex_cdc8892fe39a88051ed80f674eed8b1e.gif) = 1.6818 = 1.6818 |
| A# | ![\frac{1}{\sqrt[12]{2}^{10}}](https://smaeda.com/wp-content/plugins/latex/cache/tex_65d5e3e6032e9f9db8ad19dc4c899fb3.gif) = 0.5612 = 0.5612 |
![\sqrt[12]{2}^{10}](https://smaeda.com/wp-content/plugins/latex/cache/tex_64713aaa71ccc2b3e29e3baca4fa311e.gif) = 1.7818 = 1.7818 |
| B | ![\frac{1}{\sqrt[12]{2}^{11}}](https://smaeda.com/wp-content/plugins/latex/cache/tex_d9559a6f0ef988b5478aca6d7445fb80.gif) = 0.5297 = 0.5297 |
![\sqrt[12]{2}^{11}](https://smaeda.com/wp-content/plugins/latex/cache/tex_3d11d74c322b2dafc3a48d8162145db9.gif) = 1.8877 = 1.8877 |
| C | ![\frac{1}{\sqrt[12]{2}^{12}}](https://smaeda.com/wp-content/plugins/latex/cache/tex_d7d3aeacf041c0e53d3155f6df31eaae.gif) = 0.5000 = 0.5000 |
![\sqrt[12]{2}^{12}](https://smaeda.com/wp-content/plugins/latex/cache/tex_b19e9c43b542108533017706b2decc2c.gif) = 2.0000 = 2.0000 |
全ての隣り合う音の振動比を一定にすることによって、ギターのような複数の弦をもったフレット楽器を作ることができるようになりました。それではギターのフレット幅はどのように決まるのでしょうか。弦長が640mmのギターの第1フレットの長さは以下の式で求めることができます。
![640-640\times \frac{1}{{\sqrt[12]{2}}^{1}} =640\times \left(1-0.9438 \right)=35.968](https://smaeda.com/wp-content/plugins/latex/cache/tex_7f4096badbf6d91cdd592a620cf7e092.gif)
1フレットの長さは約36mmであることが判ります。
この式から弦長Lのnフレット目の長さは以下のようになります。
![L\times \left(\frac{1}{{\sqrt[12]{2}}^{n-1}} -\frac{1}{{\sqrt[12]{2}}^{n}} \right) =L\times \left(\frac{\sqrt[12]{2} -1 }{{\sqrt[12]{2}}^{n}} \right)](https://smaeda.com/wp-content/plugins/latex/cache/tex_59db4c4d68a44900c419cb3282da843d.gif)
