音律の誕生-ピタゴラス音律
ピタゴラス学派は万物の根源は数であると考え、音にも何らかの数学的規則が存在すると考えていました。
この規則を見出すために同じ長さ、同じ材質、同じ張力の2本の弦を準備し、一方の長さを変えながら同時に2本の弦を鳴らして、2本の弦が最も調和して響く長さを調べていきました。一番調和するのは弦の長さが半分の時、すなわち周波数が倍(1オクターブ上の音)になったときで、次に調和するのは弦の長さが$$ \frac{2}{3} $$になった時でした。$$ \frac{2}{3} $$は素数の中で最も小さい2とそれに次ぐ3で作られた、極めて単純な数字であることから、この数字を基本に規則を組み立てていくことにしたのです。基本となる弦の長さを1とすると、
【1回目】
$$ \frac{1}{1} \times \frac{2}{3} =\frac{2}{3} $$
【2回目】
$$ \frac{2}{3} \times \frac{2}{3} =\frac{4}{9} $$
この弦の長さは一オクターブより短いので長さを倍にしてオクターブ内に収める。
$$ \frac{2}{3} \times \frac{2}{3} \times \frac{2}{1}=\frac{8}{9} $$
【3回目】
$$ \frac{8}{9} \times \frac{2}{3} =\frac{16}{27} $$
まとめると以下の式ができあがります。
$$ \frac{{2}^{a}}{{3}^{b}} \times \frac{{2}^{1}}{{3}^{1}} \times \frac{{2}^{c}}{1} =\frac{{2}^{(a+1+c)}}{{3}^{(b+1)}} $$
前回の計算結果×固定値×補正値=計算結果(修正値は前二者の積が0.5以上ならc=0、以下ならc=1)
この計算を繰り返していくと以下の表の結果が得られます。
| 順番 | 数式 | 計算結果 | 弦の長さ | 音名 |
| 1 | $$ \frac{{2}^{0}}{{3}^{0}} $$ | $$ \frac{{2}^{0}}{{3}^{0}} = \frac{1}{1} $$ | 1.000 | C |
| 2 | $$ \frac{{2}^{0}}{{3}^{0}} \times \frac{2}{3} \times \frac{{2}^{0}}{1} $$ | $$ \frac{{2}^{1}}{{3}^{1}} = \frac{2}{3} $$ | 0.667 | G |
| 3 | $$ \frac{{2}^{1}}{{3}^{1}} \times \frac{2}{3} \times \frac{{2}^{1}}{1} $$ | $$ \frac{{2}^{3}}{{3}^{2}} = \frac{8}{9} $$ | 0.889 | D |
| 4 | $$ \frac{{2}^{3}}{{3}^{2}} \times \frac{2}{3} \times \frac{{2}^{0}}{1} $$ | $$ \frac{{2}^{4}}{{3}^{3}} = \frac{16}{27} $$ | 0.593 | A |
| 5 | $$ \frac{{2}^{4}}{{3}^{3}} \times \frac{2}{3} \times \frac{{2}^{1}}{1} $$ | $$ \frac{{2}^{6}}{{3}^{4}} = \frac{64}{81} $$ | 0.790 | E |
| 6 | $$ \frac{{2}^{6}}{{3}^{4}} \times \frac{2}{3} \times \frac{{2}^{0}}{1} $$ | $$ \frac{{2}^{7}}{{3}^{5}} = \frac{128}{243} $$ | 0.527 | B |
| 7 | $$ \frac{{2}^{7}}{{3}^{5}} \times \frac{2}{3} \times \frac{{2}^{1}}{1} $$ | $$ \frac{{2}^{9}}{{3}^{6}} = \frac{512}{729} $$ | 0.702 | F# |
| 8 | $$ \frac{{2}^{9}}{{3}^{6}} \times \frac{2}{3} \times \frac{{2}^{1}}{1} $$ | $$ \frac{{2}^{11}}{{3}^{7}} = \frac{2048}{2187} $$ | 0.936 | C# |
| 9 | $$ \frac{{2}^{11}}{{3}^{7}} \times \frac{2}{3} \times \frac{{2}^{0}}{1} $$ | $$ \frac{{2}^{12}}{{3}^{8}} = \frac{4096}{6561} $$ | 0.624 | G# |
| 10 | $$ \frac{{2}^{12}}{{3}^{8}} \times \frac{2}{3} \times \frac{{2}^{1}}{1} $$ | $$ \frac{{2}^{14}}{{3}^{9}} = \frac{16384}{19683} $$ | 0.832 | D# |
| 11 | $$ \frac{{2}^{14}}{{3}^{9}} \times \frac{2}{3} \times \frac{{2}^{0}}{1} $$ | $$ \frac{{2}^{15}}{{3}^{10}} = \frac{32768}{59049} $$ | 0.555 | A# |
| 12 | $$ \frac{{2}^{15}}{{3}^{10}} \times \frac{2}{3} \times \frac{{2}^{1}}{1} $$ | $$ \frac{{2}^{17}}{{3}^{11}} = \frac{131072}{177147} $$ | 0.740 | F |
| 13 | $$ \frac{{2}^{17}}{{3}^{11}} \times \frac{2}{3} \times \frac{{2}^{0}}{1} $$ | $$ \frac{{2}^{18}}{{3}^{12}} = \frac{262144}{531441} $$ | 0.493 | C |
13回目に最初の音の(ほぼ)1オクターブ上(0.493≒0.5)の音が現れたことから、1オクターブは12の音に分割されることになりました。
$$ \frac{2}{3} $$の弦の振動数は元の弦の$$ \frac{3}{2} = 1.5$$倍となり、現代の用語では完全5度の音になりますので、ピタゴラス音律は結果的に完全5度(半音8個上)の音を順番に並べたものと言い換えることができます。
| Oct. | C | C# | D | D# | E | F | F# | G | G# | A | A# | B |
| 0 | 1 | 2 | ||||||||||
| 1 | 3 | 4 | ||||||||||
| 2 | 5 | 6 | ||||||||||
| 3 | 7 | |||||||||||
| 4 | 8 | 9 | ||||||||||
| 5 | 10 | 11 | ||||||||||
| 6 | 12 |
上の表をみてみると連続した7つの音は2番目の音を主音とした長音階に含まれる音が並んでおり、それ以外の音はその音階における半音になっていることが判ります。12番目の音(F)から始まる7音(上記の黄色の部分)の2番目の音はCであり、連続する7つの音はF/C/G/D/A/E/B、それ以外の音はF#/C#/G#/D#/A#となっていて、それぞれハ長調(C)の構成音(長音階と半音)になっています。
このピタゴラス音律はピアノの鍵盤構成などにも反映され、その後の音律研究に極めて大きな影響を及ぼすことになりました。
響きを重視した音律へー純正律
中世になるとピタゴラス音律の基準となった完全5度以外にも響きの良い組み合わせがあることがわかってきました。
| 完全1度 | … | 振動比が1:1(同じ音) |
| 完全8度 | … | 振動比が1:2(1オクターブ上の音) |
| 完全5度 | … | 振動比が2:3(ド:ソ) |
| 完全4度 | … | 振動比が3:4(ド:ファ) |
| 長3度 | … | 振動比が4:5(ド:ミ) |
| 短3度 | … | 振動比が5:6(ド:ミ♭) |
| 長6度 | … | 振動比が3:5(ド:ラ) |
| 短6度 | … | 振動比が5:8(ド:ラ♭) |
これらの組み合わせによる響きの良さは不協和曲線(下のグラフ)によって明らかにされています。これを見ると1/1(完全1度)の次は6/5(短3度)、5/4(長3度)、4/3(完全4度)、3/2(完全5度)、5/3(長6度)、2/1(完全8度)となっていることが判ります。
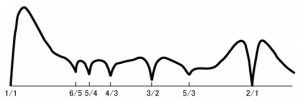
これらの組み合わせを元に作られた音律が1オクターブを整数比によって分割する「純正律」です。
| 音名 | 度数 | 1回目 | 2回目 | 3回目 | 4回目 | まとめ |
| C | 完全1度 | 1/1 | 1/1 | |||
| C# | 15/32X2 | 15/16 | ||||
| D | 4/9X2 | 8/9X1/1 | 8/9 | |||
| D# | 短3度 | 5/6 | 5/6 | |||
| E | 長3度 | 4/5 | 4/5 | |||
| F | 完全4度 | 3/4 | 3/4X1/1 | 3/4 | ||
| F# | 8/9X4/5 | 32/45 | ||||
| G | 完全5度 | 2/3 | 2/3X1/1 | 2/3 | ||
| G# | 短6度 | 5/8 | 5/8 | |||
| A | 長6度 | 3/5 | 3/5 | |||
| A# | 2/3X5/6 | 5/9 | ||||
| B | 2/3X4/5 | 8/15 | ||||
| C | 完全8度 | 1/2 | 1/2 | |||
| C# | 3/4X5/8 | 15/32 | ||||
| D | 2/3X2/3 | 4/9 |
まず、Cを基準としてC,D#,E,F,G,G#,A,Cが決まります(1回目)。次にGを基準としてA#,B,Dが決まります(2回目)。続いてDを基準としてF#が決まります(3回目)。最後にFを基準としてC#が決まります(4回目)。
| 音名 | まとめ | 弦長 | 振動数 | 振動比 |
| C | 1/1 | 1.000 | 1.000 | – |
| C# | 15/16 | 0.938 | 1.067 | 1.067 |
| D | 8/9 | 0.889 | 1.125 | 1.055 |
| D# | 5/6 | 0.833 | 1.200 | 1.067 |
| E | 4/5 | 0.800 | 1.250 | 1.042 |
| F | 3/4 | 0.750 | 1.333 | 1.067 |
| F# | 32/45 | 0.711 | 1.406 | 1.055 |
| E | 4/5 | 0.800 | 1.250 | 1.042 |
| F | 3/4 | 0.750 | 1.333 | 1.067 |
| F# | 32/45 | 0.711 | 1.406 | 1.055 |
| G | 2/3 | 0.667 | 1.500 | 1.067 |
| G# | 5/8 | 0.625 | 1.600 | 1.067 |
| A | 3/5 | 0.600 | 1.667 | 1.042 |
| A# | 5/9 | 0.556 | 1.800 | 1.080 |
| B | 8/15 | 0.533 | 1.875 | 1.042 |
| C | 1/2 | 0.500 | 2.000 | 1.067 |
| C# | 15/32 | 0.469 | 2.133 | 1.067 |
| D | 4/9 | 0.444 | 2.250 | 1.055 |
振動数比が一定になっていないため、転調がうまくできないことが判ります。それでは和音はどうなっているのでしょうか。
| 音名 | 弦長 | 振動数 | Ⅰ(C/E/G) | Ⅳ(F/A/C) | Ⅴ(G/B/D) |
| C | 1/1 | 1/1 | 1/1X4=4 | ||
| D | 8/9 | 9/8 | |||
| E | 4/5 | 5/4 | 5/4X4=5 | ||
| F | 3/4 | 4/3 | 4/3X3=4 | ||
| G | 2/3 | 3/2 | 3/2X4=6 | 3/2X8/3=4 | |
| A | 3/5 | 5/3 | 5/3X3=5 | ||
| B | 8/15 | 15/8 | 15/8X8/3=5 | ||
| C | 1/2 | 2/1 | 2/1X3=6 | ||
| D | 4/9 | 9/4 | 9/4X8/3=6 |
主要三和音全ての周波数比が4:5:6となっており、純正律が和音を重視して作られていることが判ります。
演奏性の向上を目指して-平均律とフレット長
ピタゴラス音律以来、1オクターブは12分割されることになりました。純正律も同様に12分割されていますが、ピタゴラス音律同様、音と音の振動比が一定でないために、移調ができないなどの演奏上の問題がありました。それぞれの音の周波数比を一定し、1オクターブを12分割するためには、以下の式を満たすXを求めれば良いことになります。
$$ X^{12}=2 $$
$$ X=\sqrt[12]{2}=1.059463… $$
平均律の全ての音の並びは以下の表のようになります。
| 音名 | 弦長 | 振動数 |
| C | $$ \frac{1}{\sqrt[12]{2}^{0}} $$ = 1.0000 | $$ \sqrt[12]{2}^{0} $$ = 1.0000 |
| C# | $$ \frac{1}{\sqrt[12]{2}^{1}} $$ = 0.9439 | $$ \sqrt[12]{2}^{1} $$ = 1.0595 |
| D | $$ \frac{1}{\sqrt[12]{2}^{2}} $$ = 0.8909 | $$ \sqrt[12]{2}^{2} $$ = 1.1225 |
| D# | $$ \frac{1}{\sqrt[12]{2}^{3}} $$ = 0.8409 | $$ \sqrt[12]{2}^{3} $$ = 1.1892 |
| E | $$ \frac{1}{\sqrt[12]{2}^{4}} $$ = 0.7937 | $$ \sqrt[12]{2}^{4} $$ = 1.2599 |
| F | $$ \frac{1}{\sqrt[12]{2}^{5}} $$ = 0.7492 | $$ \sqrt[12]{2}^{5} $$ = 1.3348 |
| F# | $$ \frac{1}{\sqrt[12]{2}^{6}} $$ = 0.7071 | $$ \sqrt[12]{2}^{6} $$ = 1.4142 |
| G | $$ \frac{1}{\sqrt[12]{2}^{7}} $$ = 0.6674 | $$ \sqrt[12]{2}^{7} $$ = 1.4983 |
| G# | $$ \frac{1}{\sqrt[12]{2}^{8}} $$ = 0.6300 | $$ \sqrt[12]{2}^{8} $$ = 1.5874 |
| A | $$ \frac{1}{\sqrt[12]{2}^{9}} $$ = 0.5946 | $$ \sqrt[12]{2}^{9} $$ = 1.6818 |
| A# | $$ \frac{1}{\sqrt[12]{2}^{10}} $$ = 0.5612 | $$ \sqrt[12]{2}^{10} $$ = 1.7818 |
| B | $$ \frac{1}{\sqrt[12]{2}^{11}} $$ = 0.5297 | $$ \sqrt[12]{2}^{11} $$ = 1.8877 |
| C | $$ \frac{1}{\sqrt[12]{2}^{12}} $$ = 0.5000 | $$ \sqrt[12]{2}^{12} $$ = 2.0000 |
全ての隣り合う音の振動比を一定にすることによって、ギターのような複数の弦をもったフレット楽器を作ることができるようになりました。それではギターのフレット幅はどのように決まるのでしょうか。弦長が640mmのギターの第1フレットの長さは以下の式で求めることができます。
$$ 640-640\times \frac{1}{{\sqrt[12]{2}}^{1}} =640\times \left(1-0.9438 \right)=35.968 $$
1フレットの長さは約36mmであることが判ります。
この式から弦長Lのnフレット目の長さは以下のようになります。
$$ L\times \left(\frac{1}{{\sqrt[12]{2}}^{n-1}} -\frac{1}{{\sqrt[12]{2}}^{n}} \right) =L\times \left(\frac{\sqrt[12]{2} -1 }{{\sqrt[12]{2}}^{n}} \right) $$
弦長と振動数の関係
弦の基準振動数は以下の式で求められます。
$$ \nu=\frac{ 1 }{ 2l }\sqrt{\frac{ T }{ \rho }} $$
| $$ \nu $$ | : | 振動数(Hz) |
| $$ l $$ | : | 弦長(m) |
| $$ T $$ | : | 張力(N) |
| $$ \rho $$ | : | 線密度(kg/m) |
同じ素材で同じ張力で張った弦(√内の値が一定)であれば、振動数と弦長は反比例の関係にあることが判ります。すなわち弦の長さが短くなると振動数が大きくなる(音が高くなる)のです。弦の長さが1/2になると振動数は倍になりますので、1オクターブ上の音が出るということになります。

