響きを重視した音律へー純正律
中世になるとピタゴラス音律の基準となった完全5度以外 にも響きの良い組み合わせがあることがわかってきました。
| 完全1度 | … | 振動比が1:1(同じ音) |
| 完全8度 | … | 振動比が1:2(1オクターブ上の音) |
| 完全5度 | … | 振動比が2:3(ド:ソ) |
| 完全4度 | … | 振動比が3:4(ド:ファ) |
| 長3度 | … | 振動比が4:5(ド:ミ) |
| 短3度 | … | 振動比が5:6(ド:ミ♭) |
| 長6度 | … | 振動比が3:5(ド:ラ) |
| 短6度 | … | 振動比が5:8(ド:ラ♭) |
これらの組み合わせによる響きの良さは不協和曲線(下のグラフ)によって明らかにされています。これを見ると1/1(完全1度)の次は6/5(短3度)、5/4(長3度)、4/3(完全4度)、3/2(完全5度)、5/3(長6度)、2/1(完全8度)となっていることが判ります。
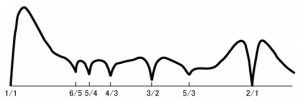
これらの組み合わせを元に作られた音律が1オクターブを整数比によって分割する「純正律」です。
| 音名 | 度数 | 1回目 | 2回目 | 3回目 | 4回目 | まとめ |
| C | 完全1度 | 1/1 | 1/1 | |||
| C# | 15/32X2 | 15/16 | ||||
| D | 4/9X2 | 8/9X1/1 | 8/9 | |||
| D# | 短3度 | 5/6 | 5/6 | |||
| E | 長3度 | 4/5 | 4/5 | |||
| F | 完全4度 | 3/4 | 3/4X1/1 | 3/4 | ||
| F# | 8/9X4/5 | 32/45 | ||||
| G | 完全5度 | 2/3 | 2/3X1/1 | 2/3 | ||
| G# | 短6度 | 5/8 | 5/8 | |||
| A | 長6度 | 3/5 | 3/5 | |||
| A# | 2/3X5/6 | 5/9 | ||||
| B | 2/3X4/5 | 8/15 | ||||
| C | 完全8度 | 1/2 | 1/2 | |||
| C# | 3/4X5/8 | 15/32 | ||||
| D | 2/3X2/3 | 4/9 |
まず、Cを基準としてC,D#,E,F,G,G#,A,Cが決まります(1回目)。次にGを基準としてA#,B,Dが決まります(2回目)。続いてDを基準としてF#が決まります(3回目)。最後にFを基準としてC#が決まります(4回目)。
| 音名 | まとめ | 弦長 | 振動数 | 振動比 |
| C | 1/1 | 1.000 | 1.000 | - |
| C# | 15/16 | 0.938 | 1.067 | 1.067 |
| D | 8/9 | 0.889 | 1.125 | 1.055 |
| D# | 5/6 | 0.833 | 1.200 | 1.067 |
| E | 4/5 | 0.800 | 1.250 | 1.042 |
| F | 3/4 | 0.750 | 1.333 | 1.067 |
| F# | 32/45 | 0.711 | 1.406 | 1.055 |
| E | 4/5 | 0.800 | 1.250 | 1.042 |
| F | 3/4 | 0.750 | 1.333 | 1.067 |
| F# | 32/45 | 0.711 | 1.406 | 1.055 |
| G | 2/3 | 0.667 | 1.500 | 1.067 |
| G# | 5/8 | 0.625 | 1.600 | 1.067 |
| A | 3/5 | 0.600 | 1.667 | 1.042 |
| A# | 5/9 | 0.556 | 1.800 | 1.080 |
| B | 8/15 | 0.533 | 1.875 | 1.042 |
| C | 1/2 | 0.500 | 2.000 | 1.067 |
| C# | 15/32 | 0.469 | 2.133 | 1.067 |
| D | 4/9 | 0.444 | 2.250 | 1.055 |
振動数比が一定になっていないため、転調がうまくできないことが判ります。それでは和音はどうなっているのでしょうか。
| 音名 | 弦長 | 振動数 | Ⅰ(C/E/G) | Ⅳ(F/A/C) | Ⅴ(G/B/D) |
| C | 1/1 | 1/1 | 1/1X4=4 | ||
| D | 8/9 | 9/8 | |||
| E | 4/5 | 5/4 | 5/4X4=5 | ||
| F | 3/4 | 4/3 | 4/3X3=4 | ||
| G | 2/3 | 3/2 | 3/2X4=6 | 3/2X8/3=4 | |
| A | 3/5 | 5/3 | 5/3X3=5 | ||
| B | 8/15 | 15/8 | 15/8X8/3=5 | ||
| C | 1/2 | 2/1 | 2/1X3=6 | ||
| D | 4/9 | 9/4 | 9/4X8/3=6 |
主要三和音全ての周波数比が4:5:6となっており、純正律が和音を重視して作られていることが判ります。
